maths

Euler’s Formula with jubes and toothpicks

brittgow

Euler_shapes

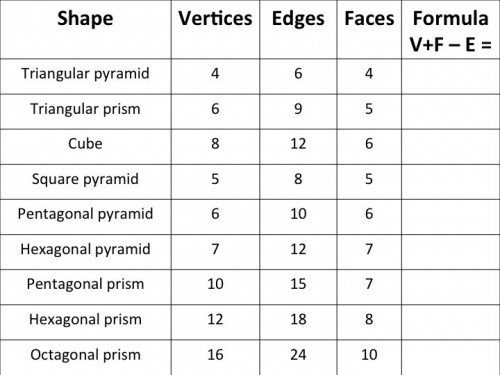
Learning Intention: To distinguish between prisms and other three-dimensional shapes and to work out the relationship between vertices, edges and faces (Euler’s Formula).

These two Year 7 students are making three-dimensional models with jubes and toothpicks (or satay sticks) to record vertices, edges and faces. Start with simple shapes, such as triangular pyramids, cubes and square pyramids, distinguishing between shapes that are prisms and those that are not. When students have made at least six or more shapes ask them to see if they can find a relationship between V (vertices); E (edges) and F (faces). I usually give a clue that they only need to use addition and subtraction (not multiplication or division).

Slide1

Great Victorian Coding Challenge

brittgow

crackthecodeImage Source

Over the next few weeks we are working with Scratch to create projects that demonstrate maths concepts using simple drag-and-drop programming. Please make sure you have completed the following steps:

1. Join Scratch with your school Username (eg gow0054) and Password. Being a registered member allows you to save and share your work. Make sure Mrs Gow has recorded your Scratch username.

2. Join the Hawkesdale P12 College Studio and the Victorian Coding Challenge (1, 2 and 3) Studios on Scratch, so you can share your work and see what other students have created.

3. Challenge #1: Create a character that draws a shape and upload to the Hawkesdale P12 College page.

4. Draw your initials, like these students in 5/6 Clark/Smith. Can you translate and reflect your initials so they appear in all four quadrats?

5. Challenge #2: Create a project that explains a maths concept. For example:

  • Draw  your initials in block letters and calculate their perimeter and the area they cover. Use the Cartesian Co-ordinate grid as a background.
  • Explain how to calculate the perimeter of a polygon or circle.
  • Name the parts of a circle (radius, diameter, circumference, sector, arc)
  • Describe different triangles (equilateral, isoceles, scalene, right-angled, acute-angled or obtuse-angled)
  • Explain how the sum of angles in a triangle always equals 180 degrees.
  • Explain how the sum of angles in a quadrilateral always equals 360 degrees
  • Explain how to calculate the area of a polygon (triangle, rectangle, parallelogram, trapezium, kite) or circle
  • Describe right angles, straight angles and complementary (adds to 90 degrees), supplementary (adds to 180 degrees) and equal angles.
  • Describe ‘pi’ and how it can be used to calculate the circumference and area of circles.
  • Describe Euler’s Rule about the faces, vertices and edges of a polyhedron (Faces + Vertices – Edges = 2)

Make sure you add your project to the Hawkesdale P12 College Studio page.

6. Challenge #3: Create a simple game that uses maths concepts. It could be something like this Hungry Fish game. Someone even created a Scratch project for Co-ordinate Grid Battleships.

Windows Apps for Maths

brittgow

windows_apps

Our Year 7 and 8 classes received Microsoft Windows tablets at the beginning of last term, as part of a DEECD trial, “Inking your Thinking”. The students have enjoyed using these devices to access Mathletics, as well as playing the “2048” game in free time at the end of a lesson. However, there are some more good Windows apps that I would like each student to download onto their devices.

Number and Algebra

  • 100 chart (for prime numbers, multiples and factors)
  • Prime factors
  • Maths Wizard
  • Easy Fractions
  • Motion Maths – Fractions
  • Motion Maths – Hungry Fish
  • Fluid Math Online
  • Dragon Box ($5.99)

Measurement and Geometry

  • Geoboard
  • Math Geometry
  • Geometry 101
  • Solve Geometry Ver 2.0

Statistics and Probability

  • Charts
  • Bar Chart creator
  • Linear graph
  • GraphPad
  • Dice Roll simulator
  • Simple coin flipper

MInecraft Maths – Surface Area and Volume

brittgow

minecraft-logo

 

Image Source

Games based learning has been a hot topic in the last year or so and one of the most popular games in educational use has been Minecraft. Although there has been some debate about the value of learning outcomes, many students would agree that Minecraft is a fun way to learn about surface area and volume. This YouTube video, “Minecraft Math – Surface Area and Volume” describes how to calculate the surface area of rectangular prisms and challenges the viewer to calculate the surface area and volume of a huge tower of TNT blocks! Another YouTube video, from the same user, demonstrates the “Volume of Prisms and Pyramids” in Minecraft and offers a challenge to calculate the area of a prism with a pyramid on top.

We spent last lesson looking at the volume and surface areas of various patterns of ‘minecraft’ blocks. Our assumption is that each Minecraft block is 1m x 1m x 1m – a cubic metre. Next lesson I would like you to create your name in Minecraft blocks and measure the volume and the surface area of your construction. Start by using the first letter of your first name. It should be a minimum of five blocks high and three blocks wide. Make sure you take a screenshot of your construction and send it to me by email.

Stem-and-Leaf Plots and Scatter plots

brittgow

Learning Intention: Students will understand what data is suitable for graphing on a scatter plot and be able to describe the significance of a “line of best fit”.

Success Criteria: You will draw a correctly labelled scatter plot from our arm span and height data and determine if there is a relationship between these measurements.

Last week you learnt the definitions for mean, median, mode and range and created a stem-and-leaf plot using the height of students in Year 7. You also measured the length of seven leaves and calculated the mean, median, mode and range of this data. This week we will investigate another type of graph, the scatter plot. Use the data we collected from our Year 7 Maths Survey to graph arm span against height (in centimeters).

This week we may also get the chance to do other activities with scatter plots:
1. Barbie Bungee
How many rubber bands are needed for Barbie to safely jump from a height of 400 cm?
What is the minimum height from which Barbie should jump if 25 rubber bands are used?
How do you think the type and width of the rubber band might affect the results?
Do you think age of the rubber bands would affect the results–that is, what would happen if you used older rubber bands?
If some weight were added to Barbie, would you need to use more or fewer rubber bands to achieve the same results?
State a possible relationship between the amount of weight added and the change in the number of rubber bands needed.
(thanks to Mrs Jirkovsky at North Adams Public School for writing about this activity on her blog!)
2. Be an actuary – distance vs earthquake intensity.

Read more →

Twelve days of Christmas in Maths!

brittgow

12_days_of_christmas

The “Twelve days of Christmas” is a popular song, with some intriguing mathematics embedded in the lyrics. 

  1. How many gifts were given in total?
  2. What was the total cost of the gifts?
  3. If one gift was returned each day following Christmas, what day would it be when there be no gifts left?

 Judy Anne Brown created this lesson plan in 1997 with some interesting explorations of Pascal’s triangle. Sol explained the mathematics of the problem in 2007 at “Wild About Math!” and another author wrote about the song and tetrahedral numbers at “The Math Less Travelled“. Create your own 12 days of Christmas image with free Christmas clip art from KidsLearnCentral.

Plan your Dream Holiday!

brittgow

aeroplane

Image source

Your task this week is to plan your dream holiday, including a schedule of places, times and dates, flights and activities as well as all the costs. You should present your work in a spreadsheet that includes meals, accommodation, flight costs, entry fees to attractions and spending money for souvenirs and gifts.

 Questions to consider:                 

(1) Where are you travelling to? Do you need a visa and/or a passport? 

(2) What dates and time of year do you plan to travel? What season will it be? 

(3) Who is travelling? By yourself, with family or friends? 

(4) How long will you be away for? 

(5) What sort of accommodation would you like? Resort, caravan park, motel, hotel, camping? How much will it cost per night? 

(6) What mode of transport will you use? Plane, car, boat, bus, train? How much will your tickets cost? 

(7) How much money do you think you need each day for food? Breakfast, lunch, dinner and snacks.

 (8) What attractions would you like visit while you are there? How much does it cost? 

(9) What time is transport available and how much will a return ticket cost?

 (10) How much spending money will you need to take per day?

Cartesian Co-ordinate Games

brittgow

battleships

Image Source

When you play battleships you are learning more than just how to blow up your partner’s ships. It is a great way to learn about cartesian co-ordinates and mapping. Here is a selection of videos about the cartesian plane or cartesian co-ordinate mapping system from Online-math-learning.  This simple maze game from Shodor Interactives requires the player to use cartesian co-ordinates to map a route to the target, avoiding the mines. The Graph Mole has two versions of the game with an animated introduction to cartesian co-ordinates. You could also use a grid on the interactive whiteboard in Elluminate or GroupBoard to set up your own battleships game with a partner. This game at “Free Online games” would be a whole lot better if it used mapping co-ordinates instead of just ‘point and click’ to the target square. IXL maths has some activities, including “points on the cartesian plane” and “co-ordinate graphs as maps“.

This one, “Co-ordinate Battleships”, created by Colin from Flying Colours Maths in UK, is especially good because it has both positive and negative co-ordinates. Play against the computer by typing the co-ordinates into the box. if anyone finds a way to play with a partner using an online whiteboard or grid co-ordinates, please let me know by leaving a comment in the chat.

Write Sums – a mobile app for maths

brittgow

write_sums_screenshot

Screenshots of Write Sums – an application for iPod Touch and iPhones

While most of the class have been starting a unit of work on Algebra, some students need to practise their basic drills. They have been enjoying using the iPod with this application, “Write Sums”. The Lite version has three different levels of difficulty and the choice of a short game (10 questions) or a long game ( 25 questions). The script recognition is pretty good, although it does get confused between “0” and “6” from time to time, which can be frustrating for the students. But it also teaches them to write neatly! This is a tactile game that they believe has improved their skills with basic operations.

Jonathon Riley has written about “The Top 10 iPod Touch Apps to Use in Maths Class“, which are all free apps. Not all of them are suitable for middle years students (iFormulas and Quick Graph are probably for older students), but they are recommended for hand-held practise.

Maths in the AFL

brittgow

Geelong_AFL

Image Source

Congratulations to the Penshurst and Hawkesdale/Macarthur U16 teams on their performance in the grand final at Lake Bolac on Saturday. We are coming up to AFL grand finals too soon, so it is a good time to look at some of the maths involved in football. Ian Lowe, from the Maths Association of Victoria, has produced a free resource for upper primary and lower secondary students, with lots of current pictures and maths problems. You can download the free resource at the MAV site. Year 7 students can access the booklet on the Student Public Drive: 6/7 Maths Folder. You can print it out (22 pages with lots of pictures) but I would prefer that you copy the word file onto your netbooks and complete the questions on your computer. When you have finished, rename the document with your name (eg. JamesAFL) and  email me the file.

Grade 6 students will need to complete this survey about the 1:1 netbook trial and this literacy and numeracy survey.