There are many skills to learn to master Algebra, but we have already made a great start – You :
1. Can recognise and continue a pattern
2. Understand that a pro-numeral (a letter) represents a variable (changing number)
3. Understand that it is mathematical convention to leave out the multiplication sign in expressions and equations involving pro-numerals.
4. Can substitute positive and negative numbers into an equation
5. Can plot points on a cartesian plane
6. Can determine the equation from a table of values
7. Can solve an equation using backtracking
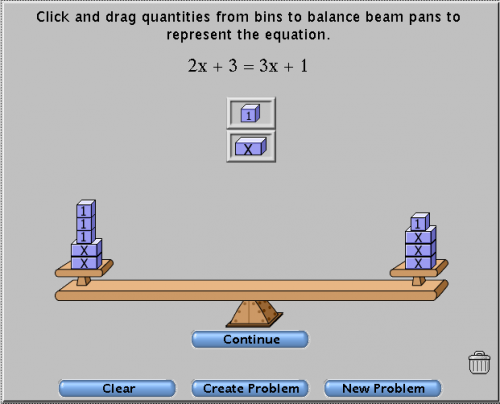
The next step is to be able to solve an equation by doing the same operation to both sides. Try these online activities:
Algebra Balance Scales (a virtual manipulative from Utah State University)
Algebra Balance Scales with negatives (same as above, but with negative numbers)
Equation Buster – from MathsNet